CADプログラムシリーズ（5）円弧の描画2

はじめに
判定の必要性
実装手順
実行結果の確認
まとめ

はじめに

前回の記事では、3点を指定して円弧を描画する方法を解説しました。しかし、ユーザーが指定した座標に基づいて、円弧が時計回りなのか反時計回りなのか、または描画するのが大円か小円かを判定する必要があります。今回の記事では、これらの判定方法について解説し、コードに実装する方法を紹介します。

判定の必要性

指定された点がどの順序で並んでいるかによって円弧の方向及び大きい方の弧（大円）または小さい方の弧（小円）が決まります。これを間違えると、前回の結果のように、期待した形状とは異なる描画結果になります。

わかりやすくするためい、ユーザ指定した３点を赤い円で表示します。今回の実行結果は以下となります。

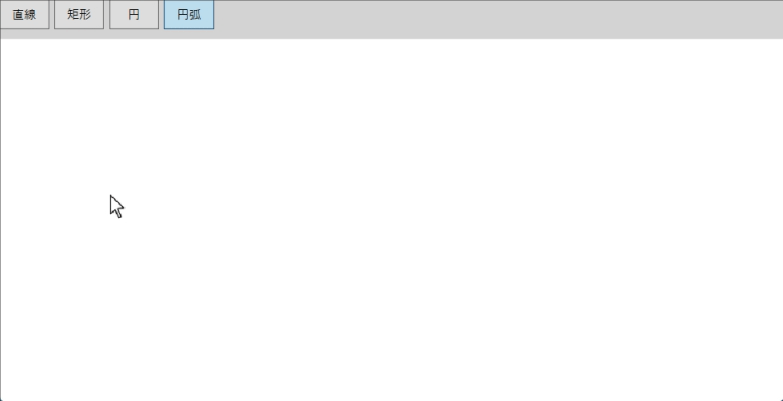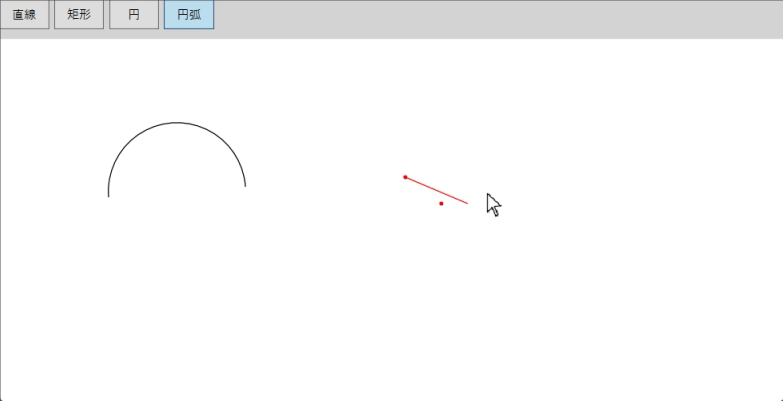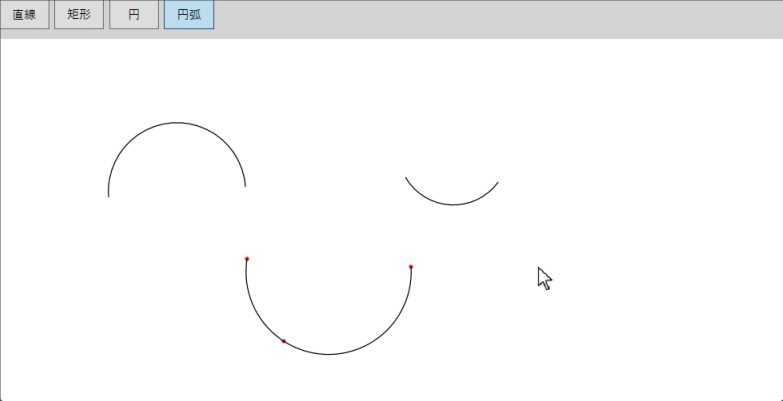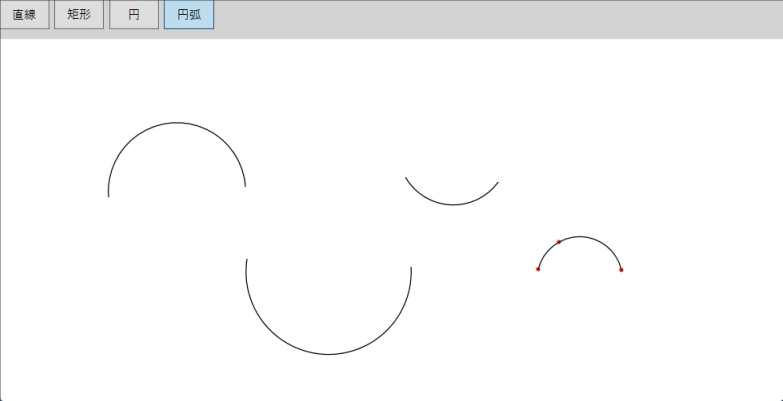
実装手順

1. 円弧の方向判定ロジック

3点が時計回りか反時計回りかを判定するには、ベクトルの外積を使用します。外積の符号によって点の並び順を判定できます。

GeometryHelperクラスに以下関数を追加します。

/// <summary>
        /// 時計回りか反時計回りかを判定
        /// </summary>
        /// <param name="p1"></param>
        /// <param name="p2"></param>
        /// <param name="p3"></param>
        /// <returns></returns>
        public static bool IsClockwise(Point p1, Point p2, Point p3)
        {
            double crossProduct = (p2.X - p1.X) * (p3.Y - p1.Y) - (p2.Y - p1.Y) * (p3.X - p1.X);
            return crossProduct > 0; // 正の場合は時計回り
        }

この関数 IsClockwise は、3つの2次元座標点 p1, p2, p3 が構成する順序が 時計回り (Clockwise) か 反時計回り (Counterclockwise) かを判定するものです。

※図形描画する時、一番左上は原点(0,0)になるため、ここでは正の場合は時計回りになります。

2. 大円と小円の判定ロジック

GeometryHelperクラスに以下関数を追加します。

この関数 IsLargeArc は、円の中心点 center、円上の開始点 start、終了点 end、および時計回りかどうかを示すフラグ isClockwise を受け取り、それらが構成する弧が 大円 (180度以上の弧) かどうかを判定します。

/// <summary>
        /// 大円かどうか判別
        /// </summary>
        /// <param name="center">円の中心</param>
        /// <param name="start">開始点</param>
        /// <param name="end">終了点</param>
        /// <param name="isClockwise">時計回りフラグ</param>
        /// <returns></returns>
        public static bool IsLargeArc(Point center, Point start, Point end, bool isClockwise)
        {
            double startAngle = Math.Atan2(start.Y - center.Y, start.X - center.X);
            double endAngle = Math.Atan2(end.Y - center.Y, end.X - center.X);

            double angle = Math.Abs(endAngle - startAngle);
            if(angle > Math.PI)
            {
                angle = Math.PI * 2 - angle;
            }

            var s = ((center.X - start.X) * (center.Y + start.Y) + (end.X - center.X) * (end.Y + center.Y) + (start.X - end.X) * (start.Y + end.Y)) / 2;
            if (s > 0 ^ isClockwise)
            {
                angle = 2 * Math.PI - angle;
            }

            return Math.Abs(angle) > Math.PI;
        }

処理の流れ

1. 開始角度と終了角度を計算

まず、開始点と終了点を中心点を基準にした角度 (ラジアン) に変換します。

double startAngle = Math.Atan2(start.Y - center.Y, start.X - center.X);
double endAngle = Math.Atan2(end.Y - center.Y, end.X - center.X);

Math.Atan2(y, x) は、点 (x,y)(x, y)(x,y) が原点を基準とした角度を計算します。
startAngle: 開始点の角度
endAngle: 終了点の角度

2. 2点間の角度差を計算

開始角度と終了角度の差を絶対値で計算し、それが π(180度) を超えている場合は補正します。

double angle = Math.Abs(endAngle - startAngle);
if (angle > Math.PI)
{
    angle = Math.PI * 2 - angle;
}

ここでの補正により、角度差は常に 0 から π の範囲になります。

3. 面積の符号による方向の確認

三角形の符号付き面積を使って、弧の方向を確認します。符号付き面積は次の式で計算されます:

var s = ((center.X - start.X) * (center.Y + start.Y) 
       + (end.X - center.X) * (end.Y + center.Y) 
       + (start.X - end.X) * (start.Y + end.Y)) / 2;

面積 s の符号:
- s>0: 反時計回り
- s<0: 時計回り
^ isClockwise により、弧の方向が指定された isClockwiseis と一致しているかを判定します。

4. 補正された角度の再計算

方向が isClockwise と異なる場合、角度を補正します:

if (s > 0 ^ isClockwise)
{
    angle = 2 * Math.PI - angle;
}

5. 弧が大円かどうかを判定

最終的に、弧の角度が π より大きいかどうかで、大円かどうかを判定します:

return Math.Abs(angle) > Math.PI;

3. 円弧描画の処理を修正

これらの判定ロジックを使用して、円弧描画の処理を修正します。

if(this._hiCadViewModel.ToolType == DrawToolType.Arc)
            {
                // 円弧の描画処理
                if (pointlist.Count != 3) return shape;

                var (center, radius) = GeometryHelper.CalculateCircle(pointlist[0], pointlist[1], pointlist[2]);

                var arc = new PathGeometry();
                var figure = new PathFigure { StartPoint = pointlist[0] };
                var arcSegment = new ArcSegment
                {
                    Point = pointlist[2],
                    Size = new Size(radius, radius),
                };

                var isClockwise = GeometryHelper.IsClockwise(pointlist[0], pointlist[1], pointlist[2]);
                arcSegment.SweepDirection = isClockwise ? SweepDirection.Clockwise : SweepDirection.Counterclockwise;
                arcSegment.IsLargeArc = GeometryHelper.IsLargeArc(center, pointlist[0], pointlist[2], isClockwise);
                figure.Segments.Add(arcSegment);
                arc.Figures.Add(figure);

                Path arcPath = new Path()
                {
                    Stroke = brush,
                    StrokeThickness = 1,
                };
                arcPath.Data = arc;
                shape = arcPath;
            }